머신러닝 - 로지스틱 회귀 모델 (Logistic Regression)

머신러닝을 배우는 것들 중에서 가장 첫번째로 배우는 것이 linear regression 즉 선형회귀라면

두번째로 배우는것은 바로 로지스틱 회귀 모델이다.

 

로지스틱 (logistic) 은 논리에 관련된 결정을 내려주는 모델이라고 생각하면 편하다

입력값을 받아서 이 값이 0이냐 1이냐 를 '분류'하는 방법이라고 생각하면 된다.

사실 0 혹은 1이 아니어도 다른 값으로 만들수 있지만 지금 처음 배우는 입장에서 여러가지 값 중에서 고르는것은 매우 어려운 일이기 때문에 지금 이 글에서는 두가지 중에 고르는 것을 서술한다.

 

앞의 선형회귀 모델은 loss function , 손실함수에대해서 먼저 서술하였다면

logistic regression은 출력 함수 부터 알아야한다.

 

(1) Sigmoid 함수

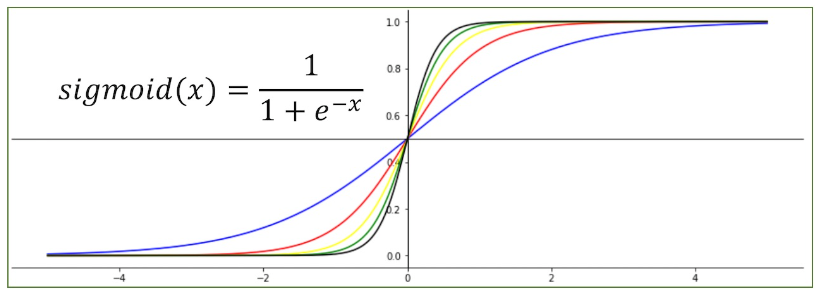
sigmoid 함수

이 함수는 보기에는 굉장히 어려운 함수 처럼 보인다.

하지만 사실은 우리는 0과 1이라는 결과값을 만들기 위해서 사용할 함수이다.

아래의 x 값 (우리가 사용할 입력값)에 따라서 0 혹은 1 사이에 있는 값들을 결과값을 가진다.

x 값이 0에서 멀어질수록 0과 1에 가까워 지고 가까워질수록 평균인 0.5에 가까운 값을 가지는 특징이 있다.

우리는 x 의 weight = a 와 bias = b를 더하여 a*x + b 의 값을 training 하는 것이 목적이다.

 

코드로 만든 sigmoid 출력함수

(2) loss function - log 함수

 

선형회귀에서는 RMSE라는 새로운 값에 대한 함수를 만들어서 loss function을 제작하였다.

하지만 logistic 회귀모델에서는 원래 우리가 알던 아주 익숙한 함수를 loss function으로 사용할것이다.

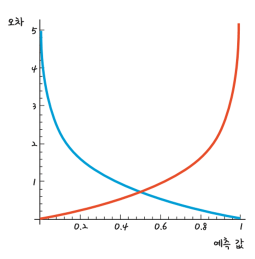
log 함수

시그모이드 함수에서 갑자기 log 함수가 튀어나오는지 의문을 가질수 있다.

하지만 log 함수의 특징을 자세히 살펴보면 처음에는 완만하게 증가하다가 점진적으로 급격하게 증가하는 모습을 관찰할 수 있다. 

그래서 만약에 y(결과) 값이 0일 때 예측값이 1에 가까워지거나 y 가 1일때 예측값이 0에 가까워질 때 오차가 급격하게 커지는 함수인것을 확인할수 있다.

 

여기서 우리는 예측값에 따라서 다른 함수를 사용해야한다. 

만약에 y 의 실제값이 1이면 파란색 그래프 -log를 사용해야하고 

반대로 y 의 실제값이 0이면 빨간색 그래프 log를 사용해야한다.

이렇게 결과에 따라서 다른 그래프를 사용해야하기 때문에 우리는 식을 새로 만들어야한다.

수식으로 만든 loss function

위의 수식은 각각의 결과에 따라서 활성화 되는 함수의 부분이 달라서

y 의 값이 오롯히 0 혹은 1로만 이루어진 logistic 모델에서는 아주 효과적으로 사용할수 있는 loss function이다.

 

앞에서 생략한 이야기이지만 sigmoid 함수에서 나온 결과값이 0과 1사이에 그어딘가에 있는 값이라고 하였는데

갑자기 결과값이 0과 1만 가진다고 하니까 당황스러울수도 있을것 같다.

하지만 우리의 최종 목표는 논리적인 분류를 해내는 것이기 때문에 결과값에서 0 혹은 1에 어디에 더 가까운 값을 가지는지를 y로 사용하는 것이다. 

예를 들면 0.7이 sigmoid 함수의 결과값이면 y = 1인 이러한 방식이다.

 

코드로 구현한 loss

(3) Training

사실 위의 두개를 모두 이해하였다면 나머지 과정은 linear regression과 동일하다.

예측 함수에다가 x 값을 넣어 나오는 값을 다시 loss function에다가 다시 넣어주면서 그 loss를 learning rate를 곱해서

weight 와 bias를 갱신해주는 그러한 방식은 여전히 동일한 것이다.

(사실 위의 내용이 머신러닝의 모든 것이라고 할 수 있다. 무엇을 결과 함수 혹은 loss function으로 사용할것인가는 각각의 데이터의 특징, 함수의 특징 등을 고려해서 사용하면 되는것이다.)

 

머신러닝 training

결과